La Espiral Aúrea.

La espiral aúrea.

La Espiral áurea es una espiral logarítmica asociada a las propiedades geométricas del rectángulo dorado. La razón de crecimiento es Φ, es decir la razón dorada. Aparece esta espiral representada en diversas figuras de la naturaleza (plantas, galaxias espirales, ), así como en el arte.

El rectángulo dorado es un rectángulo que posee una proporcionalidad entre sus lados igual a la razón aúrea. Es decir que es aquél rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado.

Desarrollo matemático:

La ecuación polar que describe la espiral dorada es la misma que cualquier otra espiral logarítmica, pero con el factor de crecimiento igual b:3

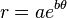o, de la misma forma

. Siendo e la base del logaritmo natural, a es una constante real positiva y b es tal que cuando el ángulo θ es un ángulo recto:

Por lo tanto, b se encuentra determinado por:

El valor numérico de b depende de si es medido con grados o como radianes; la mejor forma de encontrar una fórmula sencilla es tomar el valor absoluto de (esto es, b que puede ser también negativo):

para θ en grados;

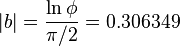para θ en radianes.

Una fórmula alternativa para la espiral dorada se obtiene en:4

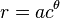donde la constante c está determinada por:

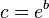para la espiral dorada los valores de c son:

si θ se mide en grados sexagesimales, y 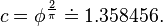si θ se mide en radianes.

La espiral Logarítmica en la naturaleza.

Aparece por primera vez en un escrito de Descartes, en 1638, aunque fue bautizada así por Jackob Bernouilli, en un trabajo suyo donde fascinado por la belleza de esta curva la llama"Spira mirabilis" , tanto le gustó que la hizo grabar en su tumba, pero en vez de poner el dibujo de la espiral logarítmica, pusieron el dibujo de la espiral de Arquímedes. Torricelli trabajó en ella independientemente y encontró la longitud de la curva.

Hace millones de años, antes de la aparición de los peces; en la familia de los cefalópodos, había muchas especies de animales con concha en forma de espiral.
También hay pruebas en el arte prehistórico irlandés (unos 3000 años a.C); y si observamos las galaxias del Universo la más cercana a nosotros es nuestra vecina Andrómeda, análogamente podemos observar la forma de la espiral en las borrascas.
En los efectos devastadores de un tornado encontramos esta curva, y los pequeños tornados que se producen en los lavabos también dibujan espirales.
Si observamos las margaritas, los girasoles, las piñas de piñones o las hojas de una rosa podemos contemplar familias enteras de espirales logarítmicas.

Construccion de la espiral aúrea.

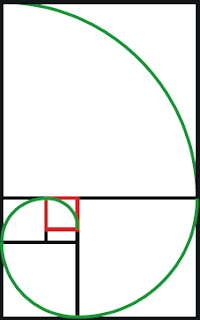
Partiendo del cuadrado CDEF contruimos un rectángulo aúreo ABEF. Si a éste le añadimos sobre un lado mayor un cuadrado, obtenemos otro rectángulo áureo BFGH.

Si después, con este rectángulo repetimos el proceso, obtenemos otro rectángulo aúreo. Este proceso se puede reproducir indefinidamente obteniendo así una sucesión de rectángulos aúreos encajados.

Una vez construida esta sucesión de rectángulos aúreos encajados, si unimos mediante un arco de circunferencia dos vértices opuestos de cada uno de los cuadrados obtenidos, utilizando como centro de la misma otro de los vértices del mismo cuadrado, obtenemos una curva muy similar a una espiral logarítmica. Es la famosa Espiral aúrea (o espiral de Durero).